Question

Given:• JK is tangent to Circle H at point J.• JHJKKH10What is the length of HK?052O 102O 10320

Answer 1

From the figure below,

HJK is an isoceles triangles with sides HJ = JK.

Also the triangle HJK is also a right angle triangle with angle 90 degrees at J.

This means that side HK is the hypotenuse.

Since HJ = JK, and HJ = 10, then JK = 10 also.

We will use the Pythagorean theorem to find HK.

From Pythagorean theorem

`\text{hyp}^2=opp^2+adj^2`

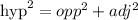
This means that

`\begin{gathered} HK^2=HJ^2+JK^2 \\ HK^2=10^2+10^2 \\ HK^2=100+100 \\ HK^2=200 \\ HK=\sqrt[]{200} \\ HK=10\sqrt[]{2} \end{gathered}`