Question

One inlet pipe can fill an empty pool in 8 hours, and a drain can empty the pool in 20 hours. How long will it take the pipe to fill the pool if the drain is left open?_____ hours

Answer 1

Given:

Time it takes the pipe to fill the pool = 8 hours

Time it takes to drain the pool = 20 hours

Let's find the time it will take the pipe to fill the pool if the drain is left open.

We have the rates as:

`\begin{gathered} \text{ }Rate\text{ to fill the pool = }(1)/(8)of\text{ the pool per hour} \\ \\ \text{ Rate to drain the pool = -}\frac{1}{20\text{ }}\text{ of the pool per hour} \end{gathered}`

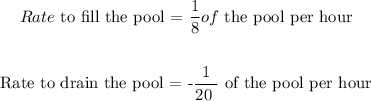
To find the time it will take to fill if the drain is left open, we have the equation:

`(1)/(8)+(-(1)/(20))=(1)/(y)`

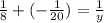
Where y represents the time it will take to fill the pool if the drain is left open.

Let's solve for y.

We have:

`\begin{gathered} (1)/(8)-(1)/(20)=(1)/(y) \\ \\ (5(1)-2(1))/(40)=(1)/(y) \\ \\ (5-2)/(40)=(1)/(y) \\ \\ (3)/(40)=(1)/(y) \end{gathered}`

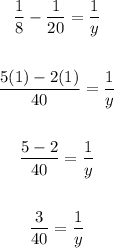
Cross multiply:

`\begin{gathered} 3y=40(1) \\ \\ 3y=40 \end{gathered}`

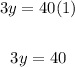
Divide both sides by 3:

`\begin{gathered} (3y)/(3)=(40)/(3) \\ \\ y=13.3hours\text{ = 13 hours }20\text{ minutes} \end{gathered}`

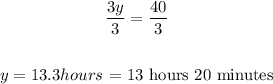
Therefore, if the drain is left open, it will take 13.3 hours for the pipe to fill the pool.

ANSWER:

13.3 hours