Question

ABCD is a parallelogram, find the missing sides or angles. (m

Answer 1

Before we can solve the length of the missing sides and measure of the missing angles, it is important to note some properties of a parallelogram.

1. The opposite angles are congruent. (∠A≅∠C, ∠B≅∠D)

2. The consecutive angles are supplementary. (∠A + ∠D = 180, ∠A + ∠B = 180, etc.)

3. The opposite sides of a parallelogram are parallel and congruent. (AD = BC, AB = DC)

4. Diagonals bisect each other. (AE = EC, DE = EB)

Based on the 2nd property, we know that ∠A + ∠D = 180°. In the question, ∠A = 120° hence, ∠D = 180° - 120° = 60°.

In the diagram, we can see that ∠D = ∠ADB + ∠BDC and the measure of ∠ADB is 43°. Let's solve for the measure of ∠BDC.

`\begin{gathered} \angle D=\angle ADB+\angle BDC \\ 60=43+\angle BDC \\ 60-43=\angle BDC \\ 17=\angle BDC \end{gathered}`

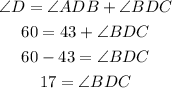
Hence, the measure of ∠BDC is 17°. Since ∠BDC and ∠ABD are alternating interior angles, the measure of ∠ABD is also 17°.

Lastly, based on the 4th property which states that diagonal bisect each other, the measure of AE is equal to the measure of EC. Since EC is 7 units, AE is also 7 units.