Answer:

For an equation to be perpendicular, the slope must be the negative reciprocal of the other equation.
Given that the slope of the line y = 1/3x + 5 is 1/3,
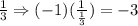
Now we have a slope of -3, we will use the following equation to find the y-intercept of the equation:

Using the point (8, -20)
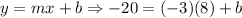

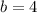
Now we got the y-intercept 4. Substituting this to the equation

And we will get:

Therefore, the equation of the line that passes through the point (8, -20) and is perpendicular to the line y = 1/3x + 5 is:
