Question

I need help with my math

Answer 1

Consider the given system of equations,

`\begin{gathered} y=2x+7 \\ 2x+5y=10 \end{gathered}`

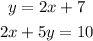
The point (-2,3) will be a solution of the system, if it satisfies both the equations of the system.

Check if point (-2,3) satisfies the first equation,

`\begin{gathered} y=2x+7 \\ 3=2(-2)+7 \\ 3=-4+7 \\ 3=3 \end{gathered}`

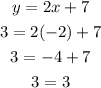
The result obtained is true, so the point (-2,3) satisfies the first equation.

Check if point (-2,3) satisfies the second equation,

`\begin{gathered} 2x+5y=10 \\ 2(-2)+5(3)=10 \\ -4+15=10 \\ 11=10 \end{gathered}`

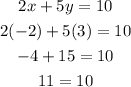
The result obtained is false, so the point (-2,3) does not satisfy the first equation.

Since the point (-2,3) fails to satisfy both the equations, so it cannot be a solution for the given system of equations.

So the correct option is 'NO'.