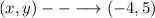1 Answer

Ask a Question

Fletcher · Answer 1 · 2023-05-15T11:15:03+0000

Solution

Use substitution to solve the system of equations given below.

y = -2x - 3

x +4y = 16

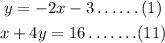
$\begin{gathered} y=-2x-3\ldots\ldots(1) \\ x+4y=16\ldots\ldots.(11) \end{gathered}$

Substitute -2x-3for y in last equation and solve for x. Insert that value into the first equation and solve for y. Check by inserting both values into the second equation.

$\begin{gathered} x+4y=16 \\ x+4(-2x-3)=16 \\ open\text{ the bracket} \\ x-8x-12=16 \\ -7x-12=16 \\ \text{collect like terms} \end{gathered}$
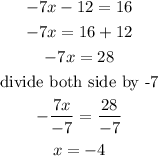
$\begin{gathered} -7x-12=16 \\ -7x=16+12 \\ -7x=28 \\ \text{divide both side by -7} \\ -(7x)/(-7)=(28)/(-7) \\ x=-4 \end{gathered}$

solve for the value of y be replacing x with -4

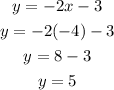
$\begin{gathered} y=-2x-3 \\ y=-2(-4)-3 \\ y=8-3 \\ y=5 \end{gathered}$

Hence the solution of the system of equations are (- 4 ,5)

$(x,y)--\longrightarrow(-4,5)$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions