Question

Leah solves the equation 3=50 by making the graph shown and finding the point of intersection. Use the drop-down menus to complete the statement below about the solution to the equation.1st drop-down menu: exactly at and around2nd drop-down menu: approximately and exactly3rd drop-down menu: 3.65, 50 and (3.65,50)

Answer 1

The equation we have is:

`3^x=50^{}`

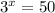
To solve this equation we need to find a value of x for which the result is 50.

By graphing

`y=3^x`

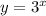
and also

`y=50`

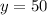
When you find the intersection between those lines, you will find the solution of the initial equation, which is what Leah is doing.

---

The graphs intersect at the point (3.56, 50) in this point 3.56 represents the x-value and 50 represents the y-value, thus for 3.56 the result of the equation is 50.

Solving the statement:

In the first option ''exactly at'' is the correct choice because the intersection between the graphs is exact and not an approximation.

In the second drop-down menu, ''exactly'' is again the correct choice because the intersection is exact and not approximate.

In the third drop-down menu, remember that the equation was

`3^x=50^{}`

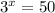
And since the intersection is at (3.56, 50) this means that when the value of x is 3.56, the value of y is 50, thus the solution for the equation is exactly 3.56, for the third menu 3.56 is the correct choice.