When we multiply a vector by a constant, if the absolute value of the constant is bigger than 1, the magnitude of the vector increases, if the absolute value of the constant is less than 1, the magnitude of the vector decreases.
![\begin{gathered} k\in\mathbb{R} \\ k>1\implies|\vec{v}|<|k\vec{v}| \\ k<1\operatorname{\implies}\lvert\vec{v}\rvert>\lvert k\vec{v}\rvert \end{gathered}]()
And if the vector is multiplied by a positive number, the vector keeps its direction. If the vector is multiplied by a negative number, the vector changes its direction.
We're multiplying a vector by minus pi. Since we have
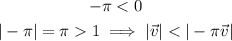
The vector will change direction and increase in magnitude.