The two buses traveled over the same time.
Recall the formula to calculate distance:
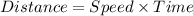
Therefore, the first bus will travel a distance:
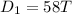
and the second bus will travel a distance of:
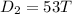
If the buses are 388.5 miles apart, then we have that:
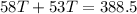
Solving, we can solve as follows:
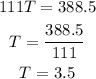
The two buses will be 388.5 miles apart after 3.5 hours.