Question

A rectangular parallelepiped whose base is 12 by 20 is inscribed in a sphere of diameter 25. Find the volume the volume of the part of the sphere outside the parallelepiped.

Answer 1

Step 1

A rectangular parallelepiped It is a three-dimensional box-shaped structure. The length of all the parallel edges here are equal.

Step 2:

The rectangular parallelepiped has the dimensions:

12 by 20 by 25

`\begin{gathered} \text{Volume of the rectangular parallelepiped } \\ =\text{ 12 }*\text{ 20 }*\text{ 25} \\ =\text{ 6000} \end{gathered}`

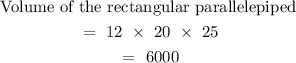
Step 3

Find the volume of a sphere with a diameter 25

Radius = 12.5

`\begin{gathered} \text{Volume of a sphere = }(4)/(3)\pi r^3^{} \\ =\text{ }(4*3.14*12.5^3)/(3) \\ =\text{ 8177.08 } \end{gathered}`

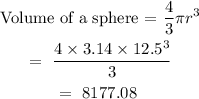
Final answer

The volume of the part of the sphere outside the parallelepiped

= 8177.08 - 6000

= 2177.08