a. Probability that the student got a B = 24/54 = 0.444444
= 0.4444 (4 decimal places)
b. Probability that the student was female AND got an "A":
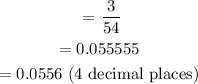
c.
Probability that the student was male OR got a "B"
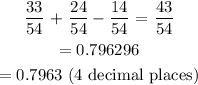
d. Probability that the student got an 'B' GIVEN they are female
