Question

Factor the polynomial if possible. If the expression be factored enter the expression

Answer 1

Since this is a quadratic polynomial of the form:

`P(x)=ax^2+bx+c`

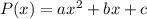
We can use the quasratic formula to get the factors of the polynomial.

The quadratic formula is:

`x_(1,2)=\frac{-b\pm\sqrt[\square]{b^2-4\cdot a\cdot c}}{2\cdot a}`

In this case, a = 6, b = -5, c = -6

Then:

`\begin{gathered} x_(1,2)=\frac{-(-5)\pm\sqrt[\square]{(-5)^2-4\cdot6\cdot(-6)}}{2\cdot6} \\ \end{gathered}`

Then solve:

`\begin{gathered} x_(1,2)=\frac{5\pm\sqrt[\square]{25^{}-(-144)}}{12} \\ x_(1,2)=\frac{5\pm\sqrt[\square]{169}}{12} \\ x_(1,2)=(5\pm13)/(12) \end{gathered}`

Now we can find the two roots:

`\begin{gathered} x_1=(5+13)/(12)=(18)/(12)=(3)/(2) \\ x_2=(5-13)/(12)=-(8)/(12)=-(2)/(3) \end{gathered}`

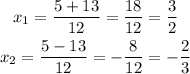
Then the factored form of the polynomial is:

`P(x)=(x-(3)/(2))(x+(2)/(3))`

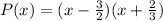
With p as the variable:

`6p-5p-6p=(p-(3)/(2))(p+(2)/(3))`