Question

I need help on problem 1. To find the work done on the gas in kj and finding how much energy is required for a piston to compress the gas back to its original volume with an efficiency of 32% Also in kj.

Answer 1

Answer:

1) Workdone = -7.5 kJ

2) Energy = 23 kJ

Explanations:

The number of moles of the ideal gas, n = 3 moles

Temperature, T = 273K

Let the old volume be V₁

Let the new volume be V₂

The new volume is three times as large as the old volume

That is, V₂ = 3V₁

The gas constant, R = 8.314

1) The workdone in the gas

The workdone in expanding the gas is given by the formula:

`W\text{ = -nRT ln(}(V_2)/(V_1))`

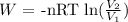
Substitute the values for this parameters into the formula above:

`\begin{gathered} W\text{ = -3}*8.314*273*\text{ ln(}(3V_1)/(V_1)) \\ W\text{ = -3}*8.314*273*\text{ ln 3} \\ W\text{ = -3}*8.314*273*\text{ 1.0986} \\ W\text{ = }-7480.55J \\ W\text{ = }(-7480.55)/(1000)kJ \\ W\text{ = }-7.48\text{ kJ} \\ W\text{ = -7.5 kJ (to the nearest 1 decimal place)} \end{gathered}`

2) The energy required for a piston to compress the gas back to its original volume with an efficiency of 32%

`\text{Efficiency = }\frac{Work}{\text{Energy}}*\text{ 100\%}`
`\begin{gathered} 32\text{ = }\frac{-7.5}{\text{Energy}}*100 \\ (32)/(100)=\text{ }\frac{-7.5}{\text{Energy}} \\ 0.32\text{ = }\frac{-7.5}{\text{Energy}} \\ \text{Energy = }(-7.5)/(0.32) \\ \text{Energy = -23.4 kJ} \end{gathered}`

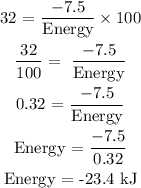
Since the piston is compressing the gas, a positive work is done on the system. Therefore, Energy = 23.4 kJ

Energy = 23 kJ (to the nearest whole number)