Question

A storage bin has the shape of a Square Prism with a Pyramid top. What is the volumeof the storage bin if its side length is s = - 9 in, the height of the prism portion ish = 16 in, and the overall height is H = 26 in?

Answer 1

To obtain the volume of the solid figure, the following steps are necessary:

Step 1: Since the figure is made up of a square base pyramid and a rectangular solid, we recall the formulas for the volumes of a square base pyramid and that of a rectangular solid, as below:

`V_{square\text{ pyramid}}=(1)/(3)* base\text{ area}* perpendicular\text{ height}`

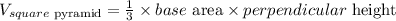
And:

`V_{rec\tan gular\text{ solid}}=length* width* height`

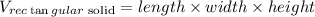
Step 2: Apply the dimensions given in the question to obtain the volumes, as follows:

Consider the rectangular solid sketched out below:

Thus, for the rectangular solid, we have that:

Length = 9in

width = 9in

height = 16in

Therefore, the volume of the rectngular solid is:

`\begin{gathered} V_{rec\tan gular\text{ solid}}=length* width* height \\ V_{rec\tan gular\text{ solid}}=9in*9in*16in \\ V_{rec\tan gular\text{ solid}}=1296in^3 \end{gathered}`

Now, consider the square base pyramid sketched out below:

Thus, for the square base pyramid, we have that:

`\text{base area = 9in}*9in=81in^2`

Also:

`\text{perpendicular height = (26in-16in)= 10in}`

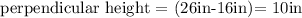
Therefore, the volume of the square base pyramid is:

`\begin{gathered} V_{square\text{ pyramid}}=(1)/(3)* base\text{ area}* perpendicular\text{ height} \\ V_{square\text{ pyramid}}=(1)/(3)*81in^2*10in \\ V_{square\text{ pyramid}}=(810)/(3)in^3 \\ V_{square\text{ pyramid}}=270in^3 \end{gathered}`

Step 3: Now, we find the total volume of the solid figure as follows:

`V_{solid\text{ figure}}=V_{rec\tan gular\text{ solid}}+V_{square\text{ pyramid}}`

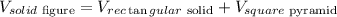
Since:

`V_{rec\tan gular\text{ solid}}=1296in^3`

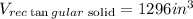
And:

`V_{square\text{ pyramid}}=270in^3`

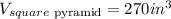
Therefore:

`\begin{gathered} V_{solid\text{ figure}}=V_{rec\tan gular\text{ solid}}+V_{square\text{ pyramid}} \\ V_{solid\text{ figure}}=1296_{}+270 \\ V_{solid\text{ figure}}=1566in^3 \end{gathered}`

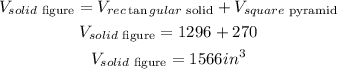
Thus, the volume of the solid figure is 1566 cubic inches