Question

Helena builds a shed in her backyard. Square based shed There is a larger section for large tools, like her lawn mower, and a smaller section for small tools. What is the length of the entire shed? What type of number is the length? List as many types of numbers for the length as you can.A=50ft^2,A=16ft^2

Answer 1

Step-by-step explanation:

Step-by-step explanation:

a) From the image attached, the area of the small section is 16ft² and the area of the large section is 50 ft². The area of a square = length × length = length².

`\begin{gathered} A_(big)=L^2 \\ L^2=50 \\ L=√(50)ft \\ A_(small)=l^2 \\ l^2=16 \\ l=√(16) \\ l=4ft \end{gathered}`

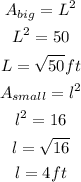
The length of the entire shed will be calculated using the formul below

`length(entireshed)=length(large)+length(small)`

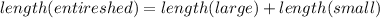
By substituting the values, we will have

`\begin{gathered} length(ent\imaginaryI reshed)=length(large)+length(small) \\ length(ent\mathrm{i}reshed)=L+l \\ length(ent\mathrm{i}reshed)=4+√(50)ft \end{gathered}`

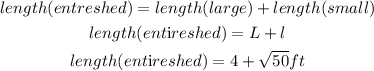
Hence,

The length of the entire shed is

`\begin{equation*} 4+√(50)ft \end{equation*}`

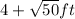
Part B:

All square root of integers other than perfect squares are irrational numbers , hence 4 + √50 is an irrational number. All numbers belongs to the set of real numbers. Therefore 4 + √50 is an irrational number and real number