Question

Rupert invested $3,000 in an account that earns a 6% annual interest rate. Find the balance of his account after 3 years compounded the following ways. Round your answers to the nearest cent

Answer 1

We have a principal of $3,000.

The annual interest rate is 6% (r=0.06).

We have to find the balance after 3 years (n=3), compounded in different ways.

The general formula, for a subperiod m, is:

`FV=PV(1+(r)/(m))^(n\cdot m)`

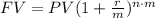
where m is the number of superiods in a year. For example, a monthly compounded interest will have m=12.

a) Annually (m=1)

`\begin{gathered} FV=PV(1+(r)/(m))^(n\cdot m) \\ FV=3000(1+(0.06)/(1))^(3\cdot1) \\ FV=3000(1.06)^3 \\ FV=3000\cdot1.191016 \\ FV\approx3573.05 \end{gathered}`

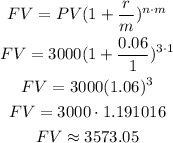
The final value is $3,573.05.

b) Semi-annually (m=2)

`\begin{gathered} FV=PV(1+(r)/(m))^(n\cdot m) \\ FV=3000(1+(0.06)/(2))^(3\cdot2) \\ FV=3000(1.03)^6 \\ FV\approx3000\cdot1.19045 \\ FV\approx3582.16 \end{gathered}`

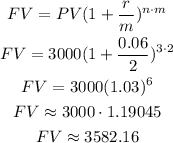
The final value when compounded semi-annually is $3,582.16.

c) Quarterly (m=4)

`\begin{gathered} FV=PV(1+(r)/(m))^(n\cdot m) \\ FV=3000(1+(0.06)/(4))^(3\cdot4) \\ FV=3000(1.015)^(12) \\ FV\approx3000\cdot1.19562 \\ FV\approx3586.85 \end{gathered}`

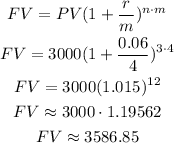
The final value when compounded quarterly is $3,586.85.

d) Monthly (m=12)

`\begin{gathered} FV=PV(1+(r)/(m))^(n\cdot m) \\ FV=3000\cdot(1+(0.06)/(12))^(3\cdot12) \\ FV=3000\cdot(1.005)^(36) \\ FV\approx3000\cdot1.19668 \\ FV\approx3590.04 \end{gathered}`

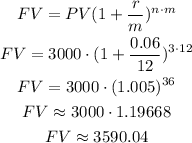
The final value when compounded monthly is $3,590.04.

Answer:

Annually: $3,573.05.

Semi-annually: $3,582.16.

Quarterly: $3,586.85.

Monthly: $3,590.04.