Question

A bicycle tire with a 12-inch radius is making 175 revolutions per minute. Find the linear speed in miles per hour.

Answer 1

Linear speed of a bicycle

Step 1: perimeter = distance in one revolution

We want to find the distance a bicycle moves in one revolution. This distance will be equal to the perimeter of its tyre.

We have that the perimeter of the tire is

perimeter = 2πr, where r is its radius

Since r = 12in, then:

perimeter = 2π · 12 in

↓

perimeter = 2 · 3.14 · 12 in ≅ 75.4 in

Step 2: finding the linear speed

We know that the bicycle tire is making 175 revolutions per minute.

Since, in one revolution the bicycle moves 75.4 in, then, in one minute it will move:

75.4 in x 175 ≅ 13,194.7 in

This is, the bicycle has a speed of 13,194.7 in per minute

Step 3: converting to miles per hour

First we convert inches to miles:

We have that 1 mile corresponds to 63,360 in.

We want to know how many miles are 13,194.7 in, then we have the following equivalence:

?? ⇄ 13,194.7 in

1 mile ⇄ 63,360 in

If we divide both sides we will have the same result:

`\frac{?\text{?}}{1}=(13,194.7)/(63,360)`

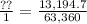
Since

`(13,194.7)/(63,360)\cong0.21`

then

`?\text{?}=(13,194.7)/(63,360)\cong0.21`

Then, the

Secondly, we convert minutes to hours:

Similarly as before we have the following equivalence:

?? ⇄ 1 min

1 hour ⇄ 60 minutes

Then