The question gives us the following system of equations:
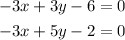
We are asked to find points that lie on these two lines represented by the equations above.
Solution
We shall solve this question simultaneously and find the values of x and y.
![\begin{gathered} -3x+3y-6=0 \\ -3x+5y-2=0 \\ \text{ Rewrite the equations.} \\ \\ -3x+3y=6\text{ (Equation 1)} \\ -3x+5y=2\text{ (Equation 2)} \\ \\ \text{Make -3x the subject of the formula in Equation 1.} \\ -3x=6-3y \\ \text{Let us substitute the expression for -3x into Equation 2.} \\ \\ -3x+5y=2 \\ (6-3y)+5y=2 \\ 6-3y+5y=2 \\ 6+2y=2 \\ \text{Subtract 6 from both sides} \\ 2y=2-6=-4 \\ 2y=-4 \\ \text{Divide both sides by 2} \\ (2y)/(2)=-(4)/(2) \\ \\ \therefore y=-2. \\ \\ \text{But we know that:} \\ -3x=6-3y \\ \text{Put the value of y into the above expression to find x.} \\ -3x=6-3(-2) \\ -3x=6+6 \\ -3x=12 \\ \text{Divide both sides by -3} \\ -(3x)/(-3)=-(12)/(3) \\ \\ \therefore x=-4 \\ \\ \\ \text{Thus, the point that lies on both lines is: }(x,y)=(-4,-2) \end{gathered}]()
Answer
The point that lies on both lines is: (-4, -2)