Question

the points (9, 21) and (18, 42) form a proportional relationship. Find the slope of the points. Then use the slope to graph the line. Answer the number of the slope

Answer 1

`\begin{gathered} \text{slope m =}(7)/(3) \\ \text{equation } \\ y=(7)/(3)x \end{gathered}`

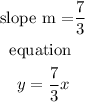
Graphing the function;

Step-by-step explanation:

Given that the points (9, 21) and (18, 42) form a proportional relationship.

`y=mx`

where; m = slope.

Given;

`\begin{gathered} (x_1,y_1)=(9,21) \\ (x_2,y_2)=(18,42) \end{gathered}`

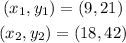
Calculating the slope;

`\begin{gathered} m=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1) \\ \text{substituting the given coordinates;} \\ m=(42-21)/(18-9) \\ m=(21)/(9) \\ m=(7)/(3) \end{gathered}`

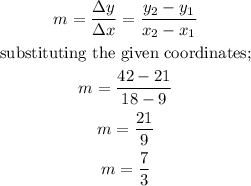
The slope of the line passing througth the points is;

`(7)/(3)`

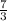
So, the equation of the proportional relationship is;

`y=(7)/(3)x`

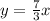
Graphing the function;