Let's list down the given information in the question.
n = 7 children
probability of a girl (p) = 0.5
Hence, we can say that probability of a boy (q) = 0.5 too.
For this situation, we can use the formula for Binomial Distribution.

To get the probability of at least 5 girls, we need to find the probability of having exactly 5, 6, and 7 girls then, add the results.
At x = 5 girls, plug in the value of n, p, q that was listed above under the given information.
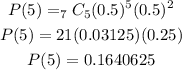
At x = 6 girls, we have:
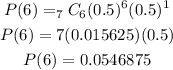
At x = 7 girls, we have:
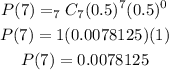
Let's add each probability to get the probability of having at least 5 girls.
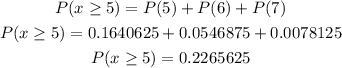
The probability of the Jones family having at least 5 girls is 0.2266.
To express the probability in percent form, let's multiply the results by 100.

Therefore, the probability of the Jones family having at least 5 girls is 22.66%.