Let's find the mean.
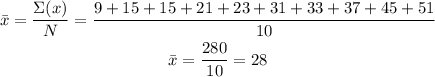
The mean is 28.
Then, we find the standard deviation
![\sigma=\sqrt[]{\frac{\Sigma(x-\bar{x})^2}{N}}](https://img.qammunity.org/2023/formulas/mathematics/college/mqawpatnmza6j30ljdoobetk0jtehpt0lr.png)
Let's find the difference between each value and the mean
9-28 = -19
15-28=-13
15-28=-13
21-28=-7
23-28=-5
31-28=3
33-28=5
37-28=9
45-28=17
51-28=23
Then, we add the square power of each subtraction
![\begin{gathered} \sigma=\sqrt[]{((-19)^2+(-13)^2+(-13)^2+(-7)^2+(-5)^2+3^2+5^2+9^2+17^2+23^2)/(10)} \\ \sigma=\sqrt[]{(1706)/(10)} \\ \sigma\approx13.1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/siq5uz7zg5bw9nucixtuixent0o9pp4nno.png)
The standard deviation is 13.1.
On the other hand, the five-number summary refers to the minimum, the first quartile, the median, the third quartile, and the maximum.
According to the given data set, we have
• The minimum is 9.
,
• The maximum is 51.
,
• The first quartile is 15. (the middle value between the first 5 numbers)
,
• The third quartile is 37. (the middle value between the second 5 numbers)
,
• The median is between 23 and 31.
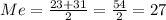
• The median is 27.