1 Answer

OwChallie · Answer 1 · 2023-10-12T03:25:04+0000

Given the Central Angle:

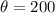
$\theta=200\text{\degree}$

And the diameter:

$d=18\operatorname{cm}$

You need to use the following formula for calculating the area of a sector of the circle:

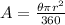
$A=\frac{\theta\pi r^2}{360\text{\degree}}$

Where "r" is the radius of the circle and θ is the Central Angle (in degrees).

By definition, the radius is half the diameter. Then:

$r=\frac{18\operatorname{cm}}{2}=9cm$

Then, substituting values into the formula and evaluating, you get:

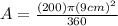
$A=\frac{(200\text{\degree)}\pi(9cm)^2^{}}{360\text{\degree}}$
$A=45\pi\text{ }\operatorname{cm}^2$

Hence, the answer is:

$A=45\pi\text{ }\operatorname{cm}^2$

Please log in or register to add a comment.