Question

The height of a projectile in feet t seconds after it is launched is given by theformula below.a. Find the maximum height attained by the projectile.b. Find the time at which the projectile hits the ground.h (t) =-16t? + 544t

Answer 1

You have the following quadratic function to determine the height of a projectile in time:

`h(t)=-16t^2+544t`

a) The maximum height is given by the y-coordinate of the vertex of the parabola (which is the representation of the given quadratic function).

Take into account that in general, a quadratic function can be written as follow:

`at^2+bt+c`

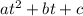
where a, b and c are coefficients.

The vertex of the function is given by:

`t=-(b)/(2a)`

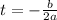
By comparing with the given function for h, you have a=-16, b=544. Replace these values into the previous formula for t:

`t=-(544)/(2(-16))=(544)/(32)=17`

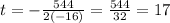
Now, replace the previous value to find h(17):

`\begin{gathered} h(17)=-16(17)^2+544(17) \\ h(17)=4624 \end{gathered}`

Hence, the maximum height reached by the projectile is 4624 feet.

b) The time at which the projectile reaches the maximum is just the value of t in the vertex of the parabola.

Hence, the time the projectile takes to reach the maximum is 17 seconds.