For this we must observe the next place value to the right (the hundredths). If it is a 4 or less, we do not take into account the following digits to the right. If it is a 5 or greater, add a 1 to the digit in the tenths place, and then remove all digits to the right. For example,
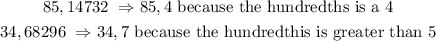
For second question, to reduce a radical, we must write in the simplest form, so that:
* The index and exponent are prime to each other. For example,
![\sqrt[3]{x^2}\text{ }\Rightarrow\text{ the index (2) and the exponent (3) are primes in this case}](https://img.qammunity.org/2023/formulas/mathematics/college/bbdtk5h7ke7k7lbtk9j36q7uva6w7lp1vr.png)
*No factor can be extracted from the radicand. For example,
![\sqrt[]{20}=\sqrt[]{4\cdot5}=\sqrt[]{4}\cdot\sqrt[]{5}=2\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/b15tr7p9oq2m66rxh4p4lzp6kemrfc55m7.png)
*The radicand has no fraction. For example,
![\sqrt[]{(5)/(4)}\Rightarrow\frac{\sqrt[]{5}}{\sqrt[]{4}}=\frac{\sqrt[]{5}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/psrkl1gfhselid74uv1leur3d86kocaa8b.png)