Let's call C the event of a weekday having sales more than $100, so the probability of this event is given by P(C) = 0.75.
Let's call C~ the complementary event (the sales being less than $100). The probability of C~ is given by:
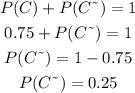
Then, if we have 3 sales, the probability of all 3 not having sales more than $100 is:
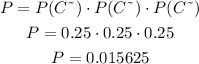
So the probability is 0.0156 or 1.56%.