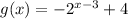For this exercise you need to remember the following Transformation Rules for functions:
1. If:
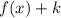
Then the function is translated "k" units up.
2. If:
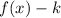
Then the function is translated "k" units down.
3. If:
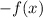
Then the function is reflected across the x-axis.
4. If:
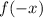
The function is reflected across the y-axis.
You have the following function f(x):
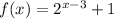
Based on the above, you know that if it is reflected across the x-axis and translated 5 units up, the function g(x) is:
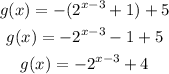
The answer is: