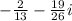Question

Divide the complex number. show all steps. reduce if possible.

Answer 1

step 1

Determine the complex conjugate of the denominator

the complex conjugate of the denominator is (6-4i)

step 2

Multiply the numerator and denominator of the fraction by the complex conjugate of the denominator

we have

`(2-5i)/(6+4i)\cdot(6-4i)/(6-4i)`

Multiply

`(2-5i)/(6+4i)\cdot(6-4i)/(6-4i)=((12-8i-30i+20i^2))/(36-16i^2)`

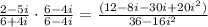
Remmeber that

i^2=-1

substitute

`\begin{gathered} ((12-8i-30i-20))/(36+16) \\ \\ (-8-38i)/(52) \\ \\ -(8)/(52)-(38)/(52)i \end{gathered}`

Simplify

`-(2)/(13)-(19)/(26)i`