Question

Probabilities of draws with replacementA fair die is rolled 4 times. What is the probability of having no 2 and no 3 among the rolls?(If necessary, consult a list of formulas.)

Answer 1

This problem is about simple probabilities with replacement, that means we are gonna have more than one trial.

In this case, we draw a fair die 4 times. The event is having no 2 and no 3 among the rolls. That means the event includes having 1, 4, 5, and 6.

So, the probability of the first draw is

`P=(4)/(6)=(2)/(3)`

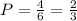
Because there are 4 events among 6 total, which won't give 2 or 3.

Now, the problem says that it's a fair die, this means all probabilities will be the same because it's the same event. So, the probability of the second draw is

`P=(2)/(3)`

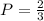
Similarly, the third and fourth draws have the same probability of 2/3 because it's a fair die.

Now, we just need to multiply all these probabilities to find the answer

`P=(2)/(3)\cdot(2)/(3)\cdot(2)/(3)\cdot(2)/(3)=(16)/(81)\approx0.20`

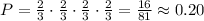
Therefore, the probability of having no 2 and no 3 among the 4 rolls is 0.20, approximately, or 20%.