27)
The given sequence is,
160, -80, 40, -20.
The first term of the sequence is a=160.
The common ratio of a sequence can be found by dividing a term by the previous term.
Hence, the common ratio is,
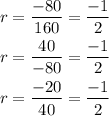
So, the common ratio is -1/2.
The n th term of a geometric sequence can be expressed as,
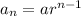
We have to find the 5th, 6th and 7th term of the given sequence.
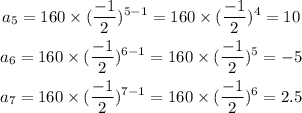
Therefore, the next three terms of the sequence 160, -80, 40, -20 is 10, -5, 2.5.
Hence, option a is correct.