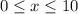The given function is
![f(x)=2\sqrt[]{-x^2+10x}](https://img.qammunity.org/2023/formulas/mathematics/college/3xjr5kdjuwwyj61thjmlbz581cooud3p6i.png)
Domain is the set of all the possible values of x, i.e domain is the input of the function
Since The x must have the value that define the function properly
SInce, x is the horizontal distance, so, x will not be negative
Thus, the x has positive real number
For the Domain of F(x)
Equate the function with zero
![\begin{gathered} 2\sqrt[]{-x^2+10x}=0 \\ \sqrt[]{-x^2+10x}=0 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hv7yx2785plmgpus6o0rgp8i1b1yi4qlzt.png)
Squaring both side
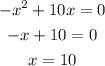
Thus, the value of x should not be greater than 10
Domain of the function is