Question

Answer the questions axis of symmetry domain and vertex ex.

Answer 1

First let's find the vertex of the equation, using the formula:

`x_v=-(b)/(2a)`

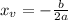
In the equation y = -x^2 - 3, we have that a = -1, b = 0 and c = -3, so:

`x_v=-(0)/(-2)=0`

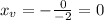
And the y-coordinate of the vertex is:

`y=-(0)^2-3=0-3=-3`

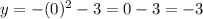
So the vertex is (0, -3).

The axis of symmetry is a vertical line that passes through the x-coordinate of the vertex.

So the axis of symmetry is x = 0.

The domain of the function is all values of x that the function can assume.

In the function y = -x^2 - 3, x can assume any value, so the domain is all real numbers.

The range of the function is all values of y that the function can assume.

The expression x^2 can only result in positive numbers, so since there is a minus sign in front of it, the maximum value of y is when we have x = 0:

`y=-0^2-3=-3`

For any other values of x, the y-value will decrease towards minus infinity. So the range is:

`\mleft\lbrace y\mright|y\le-3\}`

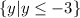
The parent function is y = x^2, so the first transformation is multiplying the function by -1, that is, the first transformation is a reflection over the x-axis.

Then, we add -3 to the function, and this represents a translation of 3 units down.

Filling the table with some ordered pairs and drawing the equation, we have: