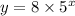Question

Write an exponential function in the form y=ab^x that goes through points (0,8) and (2, 200)

Answer 1

In this case, we need to find the constants a and b. We can find them by means of the given points.

By substituting point (0,8) into the exponential function, we have

`8=a\cdot b^0`

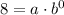
where y was equal to 8 and x was equalt to 0. Then, it yields,

`\begin{gathered} 8=a\cdot1 \\ 8=a \end{gathered}`

so, we found that a is 8.

Now, we can find b by substituting the other point with our last result. That is,

`200=8\cdot b^2`

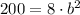
where y was 200 and x was 2. So, by moving 8 to the left hand side,we get

`\begin{gathered} (200)/(8)=b^2 \\ 25=b^2 \end{gathered}`

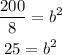
then, b is given by

`\begin{gathered} b=\sqrt[]{25} \\ b=5 \end{gathered}`

Therefore, the exponential function is

`y=8*5^x`