Solution
The general form of an exponential function is
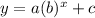
The graph of the function is inverted and shifted by 7 units to give
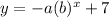
Where
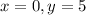
Substitute for x and y in the general form of an exponential function
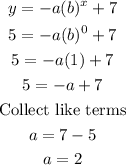
Where x = 1, y = 0.5, substitute into the function

The exponential function is
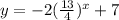
Hence,
The coefficient, a, is -2.
The base is, b, 13/4
The exponent is x
The constant, c, we adding to our function is 7