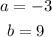Question

Determine the constants a and b so that the function f(x)=ax3+bx has a local maximum at the point: (1,6)

Answer 1

Given:

`f\mleft(x\mright)=ax^3+bx`

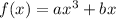
It has a local maximum at the point (1,6).

To find:

The constants a and b.

Step-by-step explanation:

Since (1, 6) is the local maximum of the function.

So, the function must be passing through the point (0, 6).

Substituting x = 1, and y = 6, we get

`\begin{gathered} 6=a(1^3)+b \\ 6=a+b \\ a+b=6..........\left(1\right) \end{gathered}`

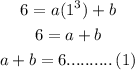
Since (1, 6) is the local maximum of the function.

So, x = 1 must be one of its critical points.

Let us find the derivative of the function.

`\begin{gathered} f^(\prime)(x)=3ax^2+b \\ f^(\prime)(1)=0 \\ 3a+b=0.........(2) \end{gathered}`

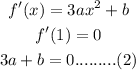
Subtracting (1) from (2), we get

`\begin{gathered} 2a=-6 \\ a=-3 \end{gathered}`

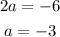
Substituting a = -3 in the equation (1) we get,

`\begin{gathered} -3+b=6 \\ b=9 \end{gathered}`

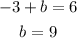
Therefore, the constants are

`\begin{gathered} a=-3 \\ b=9 \end{gathered}`

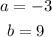
Final answer:

The constants are

`\begin{gathered} a=-3 \\ b=9 \end{gathered}`