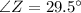Question

Please help me solve this triangle so I know I’m doing it right.

Answer 1

Let the given sides be,

x=7

y=11

z=6

To find:

`\angle X,\angle Y,\angle Z`

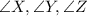
Using the formula,

`\cos X=(y^2+z^2-x^2)/(2yz)`

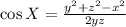
On substitution we get,

`\begin{gathered} \cos X=(11^2+6^2-7^2)/(2(11)(6)) \\ \cos X=\frac{121+36-49^{}}{132} \\ \cos X=0.81818 \\ X=\cos ^(-1)(0.81818) \\ X=35.1^(\circ) \end{gathered}`

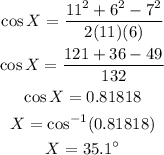
Hence, the ange of X is,

`\angle X=35.1^(\circ)`

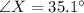
Next, we need to find the angle of y:

Using the formula,

`\cos Y=(x^2+z^2-y^2)/(2xz)`

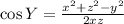
On substitution we get,

`\begin{gathered} \cos Y=(7^2+6^2-11^2)/(2(7)(6)) \\ \cos Y=\frac{49+36-121^{}}{84} \\ \cos Y=-0.42857 \\ Y=\cos ^(-1)(-0.42857) \\ Y=115.4^(\circ) \end{gathered}`

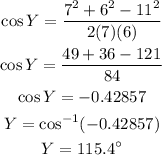
Hence, the ange of Y is,

`\angle Y=115.4^(\circ)`

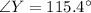
Next, we need to find the angle of Z:

Using the formula,

`\cos Z=(x^2+y^2-z^2)/(2xy)`

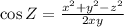
On substitution we get,

`\begin{gathered} \cos Z=(7^2+11^2-6^2)/(2(7)(11)) \\ \cos Z=\frac{49+121-36^{}}{154} \\ \cos Z=0.87012 \\ Z=\cos ^(-1)(0.87012) \\ Z=29.5^(\circ) \end{gathered}`

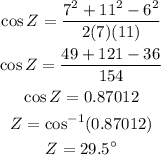
Hence, the ange of Z is,

`\angle Z=29.5^(\circ)`