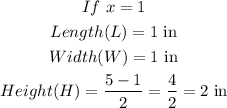From the square piece of cardboard, the length of the corners that were cut out would be:
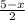
On folding the cardboard to form a box, the dimensions of the box now become:

If the volume of the box is to be 2 cubic inches, therefore,
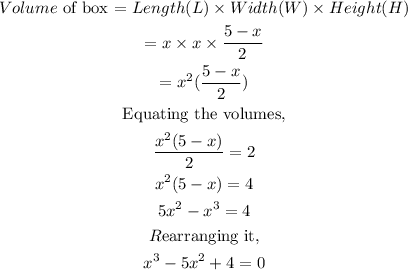
By trial and error method,
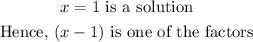
Using the polynomial long division method to find the other solution
The quotient obtained from the long division is
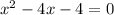
Using the quadratic formula to solve for x
![\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ \text{where, }a=1,\text{ }b=-4,\text{ }c=-4 \\ x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(-4)}}{2(1)} \\ x=\frac{4\pm\sqrt[]{16^{}+16}}{2(1)} \\ x=\frac{4\pm\sqrt[]{32}}{2} \\ x=\frac{4\pm4\sqrt[]{2}}{2} \\ x=2+2\sqrt[]{2}\text{ = }=2(1+\sqrt[]{2})\text{ =}4.828 \\ x=2-2\sqrt[]{2}\text{ = }=2(1-\sqrt[]{2})=-0.828 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/khvasjvi2ly50p17coxoyjqigekrusk0g2.png)
Hence, all the rational solutions of the equation are:
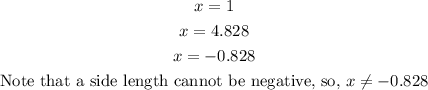
The possible side lengths of the box would be: