Question

hello can you help me solve this because I have been working on this for a while and haven't gotten the answer that is needed and thank you for your time

Answer 1

The first step we need to take in order to solve the question is to calculate the length of the wheel. The length of a circle cna be found with the following expression:

`\begin{gathered} l=2\cdot\pi\cdot r^{} \\ l=d\cdot\pi \end{gathered}`

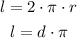
The diameter of the wheel is 24 inches, therefore:

`\begin{gathered} l=24\cdot\pi \\ l=24\pi\text{ in} \end{gathered}`

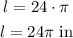
Each complete turn on the wheel moves the truck 24*pi inches. The wheel is turning at a rate of 455 rotations per minute, therefore in one minute the distance traveled by the truck is:

`\begin{gathered} v=455\cdot24\cdot\pi \\ v=10920\cdot\pi\text{ in/min} \end{gathered}`

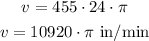
The speed of the truck is 10920*pi inches per minute. We need to convert this to miles per hour. To do that we need to divide the expression by 1056.

`\begin{gathered} v=(10920)/(1056) \\ v=10.34\cdot\pi\text{ mi/h} \end{gathered}`

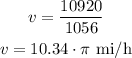
The speed of the truck in miles per hour is 10.34*pi