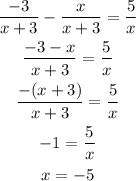We need to simplify the following equation:

The easiest way to simplify this expression is to change the side of the "x/(x+3)" term from the right to the left, because this term and the one on the left have the same denominator. Then we can directly add the numerators and conserve the denominator. We will be able to rewrite the numerator as "-(x+3)", which is the same as the denominator, but with the opposite signal resulting in -1. Then we can solve it.