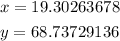Solution:
Given:
To solve for x and y,
Step 1: In ΔABC, Identify the sides of the triangle.
Thus,
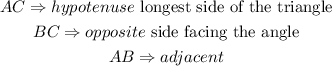
Step 2: Evaluate x, using trigonometric ratios.
From trigonometric ratios,
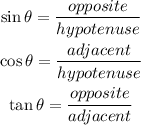
where θ = 47, we have
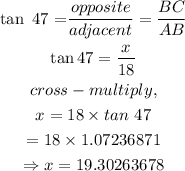
Step 4: Evaluate y, using trigonometric ratio.
Thus,
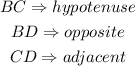
Step 3: In ΔBCD, identify the sides of the triangle.
Thus,
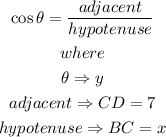
Thus, we have

Hence, the values of x and y are