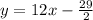The given points are (-5,3), and (7,2).
First, we have to find the slope of the line that passes through the given points.

Replacing the given points, we have
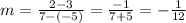
Since we have to find a perpendicular bisector to the line that passe through the given points, we have to find the perpendicular slope to -1/12.
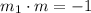
Replacing the slope, we have
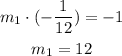
So, the perpendicular bisector has a slope of 12.
Additionally, a perpendicular bisect passes through the midpoint between (-5,3) and (7,2), so let's find it
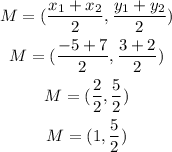
Now, we use this midpoint, the slope, and the point-slope formula to find the equation of the perpendicular bisector
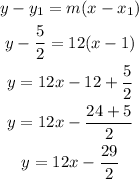
Therefore, the equation of the perpendicular bisector is