Question

Solve the right triangle. If two sides are given, give angles in degrees and minutes.

Answer 1

Concept:

The diagram below represents the question given

The given dimensions from the question are

`\begin{gathered} \angle A=10^038^(\prime) \\ c=271ft \end{gathered}`

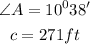
Step 1:

We will convert the angle at A from degree minutes to degree decimal

`\begin{gathered} \angle A=10^038^(\prime) \\ \angle A=10^0+(38)/(60) \\ \angle A=10^0+0.63^0 \\ \angle A=10.63^0 \end{gathered}`

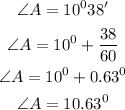
Step 2: Calculate the value of b

To calculate the value of b, we will use the trigonometric ratio below

`\begin{gathered} \cos A=\frac{Adjacent}{\text{hypotenus}} \\ \text{where,} \\ A=10.63^0 \\ \text{Adjacent}=b \\ \text{Hypotenus}=c=271ft \end{gathered}`

By substituting the values, we will have

`\begin{gathered} \cos A=\frac{Adjacent}{\text{hypotenus}} \\ \cos 10.63^0=(b)/(271) \\ \cos 10.63=(b)/(271) \\ \text{cross multiply, we will have} \\ b=\cos 10.63*271ft \\ b=266.35ft \end{gathered}`

Step 3: Calculate the value of c

To calculate the value of c, we will use the trigonometric ratio below

`\begin{gathered} \sin A=(opposite)/(Hypotenus) \\ A=10.63^0 \\ \text{opposite}=a \\ \text{Hypotenus}=c=271ft \end{gathered}`

By substituting the values, we will have

`\begin{gathered} \sin A=(opposite)/(Hypotenus) \\ \sin 10.63^0=(a)/(271) \\ \sin 10.63^0=(a)/(271ft) \\ \text{cross multiply, we will have} \\ a=\sin 10.63^0*271 \\ a=49.99ft \end{gathered}`

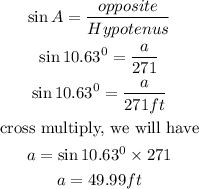
Hence,

The final answers are

a= 49.99ft

b= 266.35ft