Solution:
The function given is;
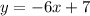
To get the ordered pair that corresponds to input-output pairs of the function, we put the input (x) into the function (y) and simplify. If the solution corresponds to the ordered pair, then it is an input-output pair of the function.
![\begin{gathered} y=-6x+7 \\ \text{Pair (2,-5) means when x = 2, y =-5} \\ \text{Putting x = 2 in the function,} \\ y=-6(2)+7 \\ y=-12+7 \\ y=-5 \\ Si\text{nce y=-5 when x = 2, then (2,-5) is an input-output pair of the function} \end{gathered}]()
![\begin{gathered} y=-6x+7 \\ \text{Pair (3,4) means when x = 3, y =}4 \\ \text{Putting x = 3 in the function,} \\ y=-6(3)+7 \\ y=-18+7 \\ y=-11 \\ Si\text{nce y=-11 when x = 3, then (3,4) is not an input-output pair of the function} \end{gathered}]()
![\begin{gathered} y=-6x+7 \\ \text{Pair (5,6) means when x = 5, y =}6 \\ \text{Putting x = 5 in the function,} \\ y=-6(5)+7 \\ y=-30+7 \\ y=-23 \\ Si\text{nce y=-23 when x = 5, then (5,6) is not an input-output pair of the function} \end{gathered}]()
![\begin{gathered} y=-6x+7 \\ \text{Pair (-6},7\text{) means when x = -6, y =}7 \\ \text{Putting x = -6 in the function,} \\ y=-6(-6)+7 \\ y=36+7 \\ y=43 \\ Si\text{nce y=43 when x = -6, then (-6,7) is not an input-output pair of the function} \end{gathered}]()
Therefore, from the above solutions, the input-output pair of the function is (2,-5)
Thus, the correct answer is option A.