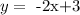To solve this problem, we should first draw a picture to grasp an idea of what is being asked. We could draw the following
we are given the black dots and we draw the line segment that passes through them. We want to find the equation of the red line. To do so, we must first note that we are told that the red line is a bisector. This means that it splits the segments into two segments that have the same length.
Using the previous fact, we can calculate the exact point through which the red line passes. It is the midpoint of the segment. Recall that given the segment that passes through the points (a,b) and (c,d), the midpoint of the segment would be the point
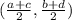
In our case, let us take a=-6,b=5,c=2, d=9. So we have that the midpoint is
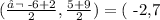
so now we know that the red line passes through the point (-2,7).
Using this fact, we can start calculating the equation of the red line. Recall that the line equation is of the form

where m is the slope and b is the y intercept. As we are told that red line is perpendicular to the black line, we should use one property of perpendicular lines:
If given lines
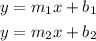
both lines are perpendicular if and only if
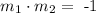
that is, the product of both slopes is equal to -1. So, in our case, to find the equation of the red line, we need its slope, which can be found through the slope of the black line.
Now, we will calculate the slope of the black line. Recall that given points (a,b) and (c,d), the slope of the line that passes through them is given by the formula
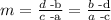
so, by taking the values as before, we have that
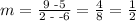
as this is the slope of the black line. We must have that the slope of the red line times this value is equal to -1. That is
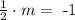
so if we multiply both sides by 2 we get

This means that the slope of the red line is -2.
Now, as we know that the red line has slope -2 and passes through the point (-2,7) we can calculate its formula. So far, we have
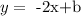
as we want this line to pass through (-2,7) we must have that when x= -2 then y = 7. So we replace this values and calculate
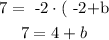
if we subtract 4 on both sides we have
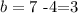
so the equation of the red line is