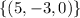Question

Saw the system of equations using matrices. Use the Gaussian elimination method with back substitution

Answer 1

From the system of equation, we construct the matrix of coefficients:

`\begin{bmatrix}{5} & {4} & {-4} & \\ {1} & {1} & {5} & \\ {1} & {-4} & {0} & 17 \\ & & & \end{bmatrix}`

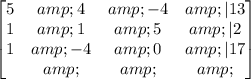
Now, we subtract the second row from the third row:

`\begin{bmatrix}{5} & {4} & {-4} & 13 \\ {1} & {1} & {5} & \\ {0} & {-5} & {-5} & \\ & & & \end{bmatrix}`

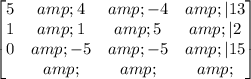
We exchange the first and the second row:

`\begin{bmatrix}{1} & {1} & {5} & 2 \\ {5} & {4} & {-4} & 13 \\ {0} & {-5} & {-5} & \\ & & & \end{bmatrix}`

Subtracting 5 times the first row from the second row:

`\begin{bmatrix}{1} & {1} & {5} & \\ {0} & {-1} & {-29} & 3 \\ {0} & {-5} & {-5} & 15 \\ & & & \end{bmatrix}`

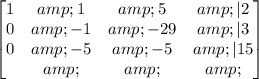
Finally, we subtract 5 times the second row from the third row:

`\begin{bmatrix}{1} & {1} & {5} & \\ {0} & {-1} & {-29} & \\ {0} & {0} & {140} & 0 \\ & & & \end{bmatrix}`

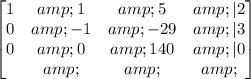
Now, using back substitution:

`\begin{gathered} 140z=0 \\ \Rightarrow z=0 \end{gathered}`
`\begin{gathered} -y-29z=3 \\ -y=3 \\ \Rightarrow y=-3 \end{gathered}`
`\begin{gathered} x+y+5z=2 \\ x-3=2 \\ \Rightarrow x=5 \end{gathered}`

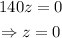
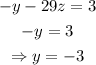
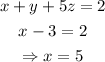
The solution set is:

`\lbrace(5,-3,0)\rbrace`