ANSWER

Step-by-step explanation
Let x be the rate of the current.
When the boat travels down the river, it travels along with the river's current. This means that the total rate is the rate of the boat plus the rate of the current:
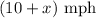
When the boat travels back up the river, it travels against the river's current. This means that the total rate is the rate of the boat minus the rate of the current:
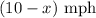
The total time the boat spends on its trip is the sum of the time it spent going down the river and back up the river.
To find the time for each, we have to apply the formula for rate (speed):

The length of the river (distance) is 21 miles. Substituting the rate for each trip into the equation and finding the sum given that the total time for the trips is 5 hours, we can write that:
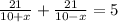
That is the equation used to solve for the rate of the current. The answer is option A.