Question

Find the value of X and each arc measurex =mAD =mBC = mDBC =

Answer 1

The total sum of the arcs in a circle is 360°. For us to be to determine the measures of arc AD, BC and DBC, let's first determine the value of x using the sum of all arcs.

`\text{ Arc AD + Arc DC + Arc CB + Arc BA = 360}^(\circ)`

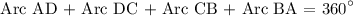
We get,

`\text{ Arc AD + Arc DC + Arc CB + Arc BA = 360}^(\circ)`
`\text{ (12x) + (17x - 14) + (2x + 5) + 90 = 360}^(\circ)`
`\text{ 12x + 17x - 14 + 2x + 5 + 90 = 360}`
`\text{ 31x + 81 = 360}`
`\text{ 31x = 360 - 81}`
`\text{ 31x = 279}`
`\text{ }\frac{\text{31x}}{31}\text{ = }\frac{\text{279}}{31}`
`\text{ x = 9}^(\circ)`

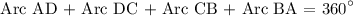
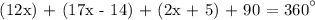
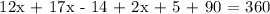
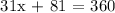
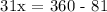
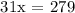
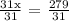
Let's use x = 9° to be able to get the measure of the three arcs.

For Arc AD,

Arc AD = 12x = 12(9) = 108°

For Arc BC,

Arc BC = 2x + 5 = 2(9) + 5 = 18 + 5 = 23°

For Arc DBC,

Arc DBC = 12x + 90 + 2x + 5 = 12(9) + 90 + 2(9) + 5 = 108 + 90 + 18 + 5 = 221°

IN SUMMARY:

x = 9°

Arc AD = 108°

Arc BC = 23°

Arc DBC = 221°