Question

I need to know the answer and how to do this

Answer 1

We are given that the lines m and n are parallel and the line t is a transversal line.

The angles given in the figure must add up to 180° as per the straight-line angle property.

So, we can set up the following equation

`(x+14)\degree+(4x-9)\degree=180\degree`

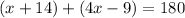
Let us solve the equation for x.

`\begin{gathered} (x+14)+(4x-9)=180 \\ x+4x+14-9=180 \\ 5x+5=180 \\ 5x=180-5 \\ 5x=175 \\ x=(175)/(5) \\ x=35 \end{gathered}`

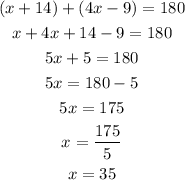
Therefore, the value of x is 35