Question

Please help me find the SA and VOLUME step by step

Answer 1

The given solid is composed of a rectangular prism and a rectangular pyramid.

The surface area of a prism is

`\begin{gathered} S_{\text{prism}}=2lw+2wh+2lh=2\cdot4\cdot8+2\cdot8\cdot3+2\cdot4\cdot3_{} \\ S_{\text{prism}}=64+48+24=136u^2 \end{gathered}`

The surface area of a rectangular pyramid is

`S_{\text{pyramid}}=A+(1)/(2)ps`

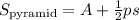
But we'll not include the area of base A because it's already included in the surface area of the prism. p is the perimeter, and s is the slant height.

`\begin{gathered} S_(pyramid)=(1)/(2)\cdot(8+4+8+4)\cdot\sqrt[]{21}=(1)/(2)\cdot24\cdot\sqrt[]{21} \\ S_{\text{pyramid}}=12\sqrt[]{21}u^2\approx55 \end{gathered}`

Then, we find the volumes. The volume of the prism is

`V_{\text{prism}}=w\cdot l\cdot h=8\cdot4\cdot3=96u^3`

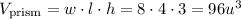
The volume of the pyramid is

`V_{\text{pyramid}}=(1)/(3)\cdot(w\cdot l)\cdot(h_1)`

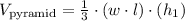
Then, the volume is

`V_{\text{pyramid}}=(1)/(3)\cdot8\cdot4\cdot(\sqrt[]{21-16})=(32)/(3)\cdot\sqrt[]{5}`