Question

Find the direction angle of v for the following vector.v=7i−2jPart 1What is the direction angle of v?

Answer 1

Given: the vector v

`v=7i-2j`

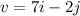
To Determine: The direction of the given vector

The vector diagram is as shown below

The direction of a vector is calculated by the formula

`\theta=\tan ^(-1)((y)/(x))`

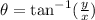
From the given vector, determine x and y

`x=7,y=-2`

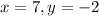
Note, the vector is on the fourth quadrant

`\begin{gathered} \theta=\tan ^(-1)((7)/(-2)) \\ \theta=74.05+270=344.05 \\ \theta\approx344.1^0 \end{gathered}`

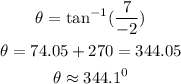
Hence, the direction of v is 344.1⁰(nearest one decimal place)