Question

What is the angle if the area is 27π and the radius is 9?

Answer 1

We have the following equation to find the area of a circle sector:

`A=((\theta)/(2\pi))\cdot\pi\cdot r^2`

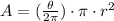
in this case, we have the following information:

`\begin{gathered} A=27\pi \\ r=9 \end{gathered}`

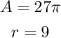
using these values on the equation and solving for theta, we get:

`\begin{gathered} ((\theta)/(2\pi))\cdot\pi\cdot(9)^2=27\pi \\ \Rightarrow(\theta)/(2)\cdot81=27\pi \\ \Rightarrow(\theta)/(2)=(27\pi)/(81)=(\pi)/(3) \\ \Rightarrow\theta=(2)/(3)\pi \end{gathered}`

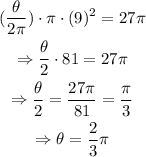
therefore, the angle is 2/3 pi. Converting to decimal, we get:

`(2)/(3)\pi\cdot(180)/(\pi)=(360)/(3)=120\degree`

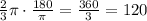
therefore, the angle measures 120 degrees